Question

Student A: √2/8 is a rational number because it can be written as a fraction Student B: √2/8 is an irrational number because √2 is irrational Evaluate the reasoning provided by both students A and B and correct the errors. Make sure to provide proper reasoning. Come up with one challenging rational or irrational number in your post. Make sure to not include the answer.

Answer 1

saysWe want to find out whether;

`\frac{\sqrt[]{2}}{8}`

Is rational or irrational.

A condition for a number to be rational is for us to be able to write the number as a fraction, i.e in the form;

`(p)/(q)`

This is subject to some caveats;

p and q have to be integers, q has to be a non-zero denominator, i.e, it cannot be zero.

The number in question is;

`\frac{\sqrt[]{2}}{8}`

Student A argues that the number is rational because it is written as a fraction, however, the numerator is irrational, and therefore, the whole number is irrational.

Student B is says that the number is irrational because the numerator is irrational, this si correct, since we can express the number as;

`\frac{\sqrt[]{2}}{8}=\sqrt[]{2}*(1)/(8)`

and multiplying an irrational number with a rational number will always result in an irrational number.

We could see for example;

`(\pi)/(2)`

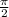
This is also a fraction, but since pi is irrational, the whole number is irrational.

Therefore, Student A is wrong and Student B is correct.