Question

The areas of two circles can be expressed as the ratio of 9 to 16. What is the ratio of their radii? O A. 81 to 256 O B. 4.5 to 8 O C. 3 to 4 O D. 18 to 32

Answer 1

We are told that the ratios between areas of two circles are 9 to 16, this means the following:

`(A_1)/(A_2)=(9)/(16)`

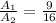
Since the area of a circle is given by the following formula:

`A=\pi r^2`

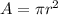
Replacing in the proportion:

`\frac{\pi r^2_{1^{}}}{\pi r^2_2}=(9)/(16)`

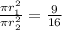
canceling out the pis:

`(r^2_1)/(r^2_2)=(9)/(16)`

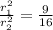
Now we use the following property of exponents:

`(a^2)/(b^2)=(^{}(a)/(b))^2`

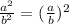
Applying the property:

`((r_1)/(r_2))^2=(9)/(16)`

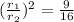
Now we take the square root to both sides:

`(r_1)/(r_2)=\sqrt[]{(9)/(16)}`

Solving:

`(r_1)/(r_2)=(3)/(4)`

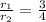
Therefore, the radius is at a proportion of 3 to 4.