Answer:
Cliff Branch bought a home with a 10.5% adjustable rate mortgage for 30 years. He paid $9.99 monthly per thousand on his original loan
So, per thousand value of $65000 is 65000/1000=65
Now, the old monthly payment was =
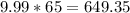
He decides to renew and will now pay $10.68 monthly per thousand on his loan.
So, the new monthly payment is =

The percent increase in his monthly payment is=
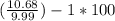 =6.906% and to nearest tenth it is 6.9%
=6.906% and to nearest tenth it is 6.9%