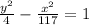Answer:
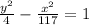
Explanation:
The standard form of hyperbola centered at origin is given by:
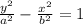 ....[1]
....[1]
where,
vertices and foci are
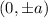 and
and
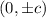 respectively.
respectively.
As per the statement:
The hyperbola with vertices at (0, ±2) and foci at (0, ±11).
⇒a = 2 and c = 11
⇒
 and
and
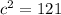
To find
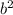 :
:
Using the equation:
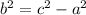
then;
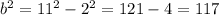
⇒
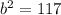
Substitute the given values in [1] we have;
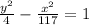
Therefore, an equation in standard form for the hyperbola with vertices at (0, ±2) and foci at (0, ±11) is,