Question

Three of the vertices of square ABCD are located at A(0,3), B(4,0), and C(7,4).

Determine the area of square ABCD.​

Answer 1

The area of the square ABCD is 25 square units

Explanation:

The square ABCD has three of its vertices at A(0,3), B(4,0), and C(7,4). The fourth vertex has been also plotted in the image attached below.

The area of the square is

`A = a^2`

Where a is the length of any of the square's sides. We only have to find the distance from any two consecutive vertices, for example, A(0,3), B(4,0):

`a=√((4-0)^2+(0-3)^2)`

`a=√(16+9)=√(25)=5`

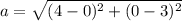
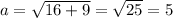
a = 5

Calculating the distance between any other pair of consecutive vertices would yield the same result. The area is now calculated:

`A = 5^2 = 25`

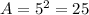
The area of the square ABCD is 25 square units