Answer:
x = 0, y = 4
Explanations:
The given system of equations is:
8x + 9y = 36............(1)
3x + 4y = 16.............(2)
Make x the subject of the formula from equation (1)
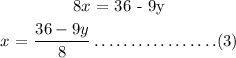
Substitute equation (3) into equation (2)

Substitute the value of x into equation (3)
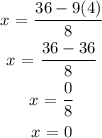
The solutions to the system of linear equations are x = 0, y = 4