Question

A central angle measuring 120° intercepts an arc in a circle whose radius is 3. What is length of the arc of the circle formed by this central angle? Round the length of the arc to the nearest hundredth of unit.

6.28 units
12.57 units
9.42 square units
6.28 degrees

Answer 1

`\bf \textit{arc's length}\\\\ s=\cfrac{\theta r\pi }{180}\qquad \begin{cases} r=radius\\ \theta=\textit{central angle in degrees}\\ s=\textit{arc's length} \end{cases}`

Answer 2

6.28 units

Explanation:

Since, the length of an arc on a circle is,

`l=r* \theta`

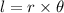
Where, r is the radius of the circle and
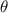`\theta` is the central angle ( in radian ) made by the arc,

Here,

r = 3 unit,

`\theta=120^(\circ)=120* (\pi)/(180)=(2\pi)/(3)\text{ radian}`

(
`\pi \text{ radian}= 180^(\circ)` )

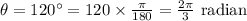
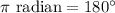Hence, the length of the given arc is,

`l=3* (2\pi)/(3)=2\pi =6.28318530718\approx 6.28\text{ units}`

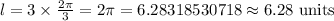
First option is correct.