Question

How to know if a function is periodic without graphing it ?

Pi * sin(pi*t/2) + 1.8cos(7*pi*t/5)

Answer 1

A function
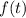
`f(t)` is periodic if there is some constant
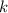
`k` such that
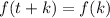
`f(t+k)=f(k)` for all
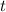
`t` in the domain of
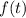
`f(t)`. Then
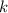
`k` is the "period" of
`f(t)`.

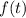
Example:

If
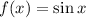
`f(x)=\sin x`, then we have
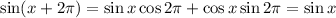
`\sin(x+2\pi)=\sin x\cos2\pi+\cos x\sin2\pi=\sin x`, and so
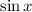
`\sin x` is periodic with period
`2\pi`.

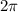
It gets a bit more complicated for a function like yours. We're looking for
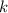
`k` such that


`\pi\sin\left(\frac\pi2(t+k)\right)+1.8\cos\left(\frac{7\pi}5(t+k)\right)=\pi\sin\frac{\pi t}2+1.8\cos\frac{7\pi t}5`

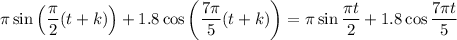
Expanding on the left, you have


`\pi\sin\frac{\pi t}2\cos\frac{k\pi}2+\pi\cos\frac{\pi t}2\sin\frac{k\pi}2`

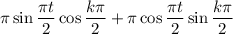
and


`1.8\cos\frac{7\pi t}5\cos\frac{7k\pi}5-1.8\sin\frac{7\pi t}5\sin\frac{7k\pi}5`

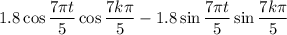
It follows that the following must be satisfied:


`\begin{cases}\cos\frac{k\pi}2=1\\\\\sin\frac{k\pi}2=0\\\\\cos\frac{7k\pi}5=1\\\\\sin\frac{7k\pi}5=0\end{cases}`

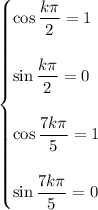
The first two equations are satisfied whenever
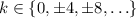
`k\in\{0,\pm4,\pm8,\ldots\}`, or more generally, when
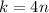
`k=4n` and
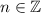
`n\in\mathbb Z` (i.e. any multiple of 4).

The second two are satisfied whenever
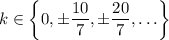
`k\in\left\{0,\pm\frac{10}7,\pm\frac{20}7,\ldots\right\}`, and more generally when
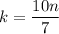
`k=\frac{10n}7` with
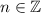
`n\in\mathbb Z` (any multiple of 10/7).

It then follows that all four equations will be satisfied whenever the two sets above intersect. This happens when
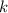
`k` is any common multiple of 4 and 10/7. The least positive one would be 20, which means the period for your function is 20.

Let's verify:


`\sin\left(\frac\pi2(t+20)\right)=\sin\frac{\pi t}2\underbrace{\cos10\pi}_1+\cos\frac{\pi t}2\underbrace{\sin10\pi}_0=\sin\frac{\pi t}2`


`\cos\left(\frac{7\pi}5(t+20)\right)=\cos\frac{7\pi t}5\underbrace{\cos28\pi}_1-\sin\frac{7\pi t}5\underbrace{\sin28\pi}_0=\cos\frac{7\pi t}5`

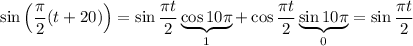
More generally, it can be shown that


`f(t)=\displaystyle\sum_(i=1)^n(a_i\sin(b_it)+c_i\cos(d_it))`

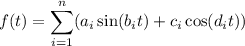
is periodic with period
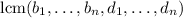
`\mbox{lcm}(b_1,\ldots,b_n,d_1,\ldots,d_n)`.