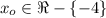Question

13. Consider the function g graphed below. For whatvalues of Xo does lim g(x) exist?

Answer 1

We will say that the limit

`\lim _(x\to xo)f(x)=a`

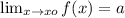
exists if we reach the same value (a) regardless of the direction we approach x_0

So, in the case of the graph, the function is evidently continuous everywhere except for two points in which we need to determine whether the function is continuous there or not.

Notice that x->-4 is one of those particular points.

We have that:

`\begin{gathered} \lim _(x-\to-4)f(x)=6 \\ \text{and} \\ \lim _(x+\to-4)f(x)=4 \end{gathered}`

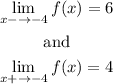
Then, we obtain the value 6 if we approach x= -4 from the left and we get 4 if we move towards x= -4 from the right. The two values are not the same, therefore the limit does not exist there.

As for x-> 2

Notice that

`\lim _(x-\to2)f(x)=2=\lim _(x+\to2)f(x)`

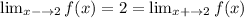
Therefore, the limit exists and it is equal to 2 even though the function has a different value there.

Therefore, the limit exists for any point in the set:

`x_o\in\mathfrak{\Re }-\mleft\lbrace-4\mright\rbrace`