Question

determine the discriminat and use it to determine the number of x-intercepts for the graph of f(x) = 2x^2 - 8x + 9

Answer 1

`\begin{gathered} x=2+i14 \\ x=2-i14 \\ \text{ Complex answer, no x-intercepts} \end{gathered}`

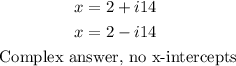
Step-by-step explanation: The discriminant is the part of the quadratic formula underneath the square root symbol As we know that square root of any number is both plus and minus of a certain value:

`\sqrt[]{a}=\pm c\Rightarrow(-c)^2=(+c)^2=a`

Using this information about the discriminant we can determine the x-intercepts of the graph as follows:

`f(x)=2x^2-8x+9=0\Rightarrow\text{ Solving this quadratic equation will give x-intercepts}`

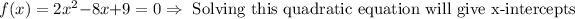
Quadratic equation solution:

`\begin{gathered} f(x)=2x^2-8x+9=0\Rightarrow x=\frac{-B\pm\sqrt[]{B^2-4AC}}{2A} \\ \because\Rightarrow \\ A=2 \\ B=-8 \\ C=9 \\ \therefore\Rightarrow \\ x=\frac{-(-8)\pm\sqrt[]{(-8)^2-(4*2*9)}}{2*(2)}=\frac{8\pm\sqrt[]{16^{}-72}}{4}=\frac{8\pm\sqrt[]{-56}}{4}=2\pm\frac{\sqrt[]{-56}}{4} \\ \therefore\Rightarrow \\ x=2\pm i14 \\ \rightarrow\text{ Complex answer} \\ x=2+i14 \\ x=2-i14 \end{gathered}`

Graph

Note! The plot of f(x) above confirms that there are no x-intercepts of this function, so the reason for complex values of x. also discriminant is the square root of -56