Question

What is the area of the two-dimensional cross section that is parallel to face ABC ?

Answer 1

The area is 84, because you want to multiply 7 and 24, then divide by 2 to find the area of a right triangle.

Answer 2

Answer: The required area is 84 square feet.

Step-by-step explanation: We are given to find the area of the two-dimensional cross section that is parallel to face ABC.

Since ABC is a right-angled triangle at ∠B = 90°, so its parallel face will also be a right-angled triangle.

And the area of the parallel face must also be equal to the area of ΔABC.

Applying Pythagoras theorem, we have from ΔABC that

`AC^2=AB^2+BC^2\\\\\Rightarrow BC^2=AC^2-AB^2\\\\\Rightarrow BC^2=25^2-7^2\\\\\Rightarrow 625-49\\\\\Rightarrow BC^2=576\\\\\Rightarrow BC=24.`

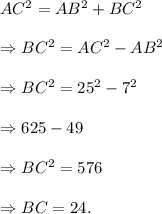
So, area of triangle ABC is

`A=(1)/(2)* base* altitude=(1)/(2)*B* BC=(1)/(2)* 7* 24=84~\textup{sq ft.}`

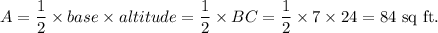
Thus, the area of the parallel face is 84 sq. ft.