Question

A bicyclist of mass 112 kg rides in a circle at a speed of 8.9 m/s. If the radius of the circle is 15.5 m, what is the centripetal force on the bicyclist?

Answer 1

Hello!

A bicyclist of mass 112 kg rides in a circle at a speed of 8.9 m/s. If the radius of the circle is 15.5 m, what is the centripetal force on the bicyclist ?

We have the following data:

Centripetal Force = ? (Newton)

m (mass) = 112 Kg

s (speed) = 8.9 m/s

R (radius) = 15.5 m

Formula:

`\boxed{F_(centripetal\:force) = (m*s^2)/(R)}`

Solving:

`F_(centripetal\:force) = (m*s^2)/(R)`

`F_(centripetal\:force) = (112*8.9^2)/(15.5)`

`F_(centripetal\:force) = (112*79.21)/(15.5)`

`F_(centripetal\:force) = (8871.52)/(15.5)`

`F_(centripetal\:force) = 572.356129...`

`\boxed{\boxed{F_(centripetal\:force) \approx 572.36\:N}}\end{array}}\qquad\checkmark`

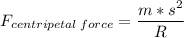
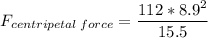
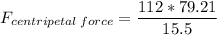
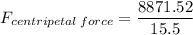
Answer:

The centripetal force on the bicyclist is approximately 572.36 N

____________________________________

I Hope this helps, greetings ... Dexteright02! =)

Answer 2

The centripetal force, Fc, is calculated through the equation,
Fc = mv²/r
where m is the mass,v is the velocity, and r is the radius.
Substituting the known values,
Fc = (112 kg)(8.9 m/s)² / (15.5 m)
= 572.36 N
Therefore, the centripetal force of the bicyclist is approximately 572.36 N.