Question

Points A(-2, 4), B(1, 3), C(4, -1) and D form a parallelogram. What are the coordinates of D? (5, 5) (0, 0) (1, -2) (1, 0) (3, 4)

Answer 1

D. (1, 0)

Explanation:

Correct for plato, trust me

Answer 2

If its a ABCD parallelogram ,
then, let , D(x,y)
so DA=
`\sqrt{(-2+x)^(2) +(4+y)^(2) }`
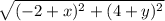
BC=
`\sqrt{(1+4)^(2)+(3-1)^(2) }`
=
`√(25+4)`
=
`√(29)`
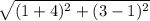
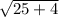
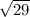
According to question ,

`\sqrt{(-2+x)^(2) +(4+y)^(2) }`=
`√(29)`
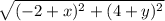
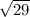
[Because, DA||BC]
or, (x-2)²+(y+4)²=29.....(1)
Again,
CD=
`\sqrt{(x+4)^(2) +(y-1)^(2) }`
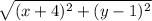
and AB=
`\sqrt{(-2+1)^(2)+(4+3)^(2) }`
=
`√(1+49)`
=
`√(50)`
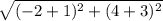
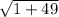
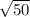
According to question,
(x+4)²+(y-1)²=50.......(2)
[Because,CD||AB]
From (1),
x²-4x+4+y²+8y+16=29
x²+y²-4x+8y=29.....(3)
from (2),
x²+8x+16+y²-2y+1=50
x²+y²+8x-2y=33.....(4)
From(3)-(4),
-12x+10y=-4
or,-6x+5y=-2
or,5y=6x-2
or,y=
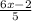
`(6x-2)/(5)`.....(5)
Again (3)+(4),
4x+6y=62
or,2x+3y=31
or,2x+
`(3(6x-2))/(5)`=31
or,
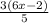
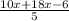
`(10x+18x-6)/(5)`=31
or,28x-6=155
or,28x=161
or,x=
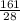
`(161)/(28)` =5.75
By putting x=
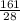
`(161)/(28)` in (5) ,
y=
`( (6X161)/(28) -2 )/(5)`
or,y=
`( (966)/(28) -2 )/(5)`
or,y=
`( (966-56)/(28) )/(5)`
or,y=
`(940)/(140)`
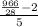
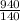
or,y=6.5
So D(x,y)=(5.75,6.5)