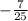Question

Suppose sin(x) = -3/5 and cos(x) < 0. What the value of cos(2x)? -16/25-7/257/2516/25

Answer 1

We have that:

`\sin (x)=-(3)/(5)`

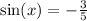
And with this information, we need to find the value of cos(2x).

To do this we use the following formula that relates sinx and cos(2x):

`\cos (2x)=1-2\sin ^2x`

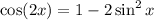
Substituting the value of sin(x):

`\cos 2x=1-2(-(3)/(5))^2`

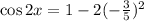
Now we need to solve the operations. We squared (-3/5) and we get (9/25):

`\cos (2x)=1-2((9)/(25))`

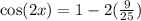
Next, we multiply 2 by (9/25) and get 18/25 instead:

`\cos (2x)=1-(18)/(25)`

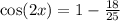
And finally, to make this substraction we consider 1=25/25

`\begin{gathered} \cos (2x)=(25)/(25)-(18)/(25) \\ \cos (2x)=(7)/(25) \end{gathered}`

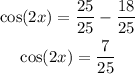
But, since we are considering that cos(x)<0 (is negative), then cos(2x) must also be negative, so the answer is:

`-(7)/(25)`