Question

Given a==1(mod 7), b== 2 (mod7), and c == 6 (mod7), what is the remainder when a^81 b^91 c^27 is divided by 7?

Answer 1

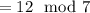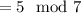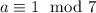
`a\equiv1\mod7` means there is an integer
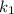
`k_1` such that
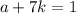
`a+7k=1`, or
`a=1-7k`.

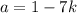
Raising both sides to an arbitrary integer power, we have


`a^n=(1-7k)^n=\displaystyle\sum_(k=0)^n\binom nk(-7k)^k`

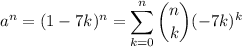
Notice that each term in the expansion on the right is a multiple of 7 when
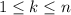
`1\le k\le n`, which means modulo 7, the right side reduces to 1. Therefore if
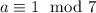
`a\equiv1\mod7`, then
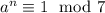
`a^n\equiv1\mod7` as well.

More generally, the remainder of a number
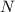
`N` upon dividing by 7 will be determined by the constant term (independent of
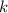
`k`) in the binomial expansion, because any term with a contributing factor of
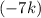
`(-7k)` necessarily is a multiple of 7.

You then have


`a\equiv1\mod7\implies a^(81)\equiv1^(81)\equiv1\mod7`

`b\equiv2\mod7\implies b^(91)\equiv2^(91)\mod7`

`c\equiv6\mod7\implies c^(27)\equiv6^(27)\mod7`

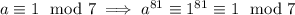
Now,


`a^(81)b^(91)c^(27)\equiv1^(81)2^(91)6^(27)\mod7=2^(118)3^(27)\mod7`

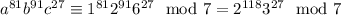
Recall that for
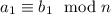
`a_1\equiv b_1\mod n` and
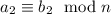
`a_2\equiv b_2\mod n`, we have
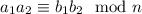
`a_1a_2\equiv b_1b_2\mod n`, which means we can determine the remainder above by multiplying the remainders given by
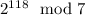
`2^(118)\mod7` and
`3^(27)\mod7`.

In particular, if
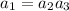
`a_1=a_2a_3`, then


`a_1\mod7=\bigg((a_2\mod7)(a_3\mod7)\bigg)\mod7`

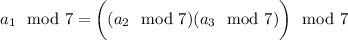
Now, we get by this property in conjunction with Fermat's little theorem that


`2^(118)\mod7=\bigg((2^(115)\mod7)(2^6\mod7)\bigg)\mod7`

`=2^(112)\mod7`

`=\bigg((2^(106)\mod7)(2^6\mod7)\bigg)\mod7`

`=2^(106)\mod7`

`=2^(100)\mod7`

`=\cdots`

`=2^4\mod7`

`=\bigg((2^3\mod7)(2\mod7)\bigg)\mod7`

`=2\mod7`


`3^(27)\mod7=\bigg((3^(21)\mod7)(3^6\mod7)\bigg)\mod7`

`=3^(21)\mod7`

`=3^(15)\mod7`

`=3^9\mod7`

`=3^3\mod7`

`=\bigg((3^2\mod7)(3\mod7)\bigg)\mod7`

`=6\mod7`

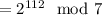
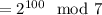
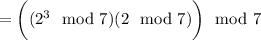
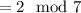
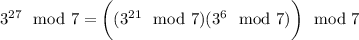
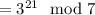
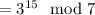
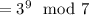
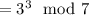
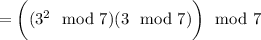
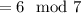
So we obtain


`2^(118)3^(27)\mod7=\bigg((2\mod7)(6\mod7)\bigg)\mod7`

`=12\mod7`

`=5\mod7`