Question

What is the oblique asymptote of the function f(x) = the quantity x squared minus 5x plus 6 over the quantity x minus 4?

Answer 1

The oblique asymptote is x-1.

Answer 2

x - 1

Explanation:

We know that, a slant or oblique asymptote of a rational function is the asymptote that helps in determining the direction of the function.

It occurs when the polynomial in the numerator is a higher degree than the polynomial in the denominator.

Now, we divide the numerator by denominator using long division method and the first two terms in the quotient ( forming a linear function ) is the equation of the oblique asymptote.

We are given the rational function,
`f(x) = (x^(2)-5x+6)/(x-4)`.

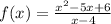After dividing we get that, the quotient is x - 1.

Hence, the equation of the oblique asymptote is x-1.