Question

How do convolutions work with a Heaviside function?

For example, if f(t) = t^2 and g(t)=u(t-1), how do I find f*g?

Answer 1

By definition, you have


`\displaystyle(f*g)(t)=\int_(-\infty)^\infty f(\tau)g(t-\tau)\,\mathrm d\tau`

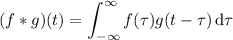
Take
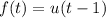
`f(t)=u(t-1)` and
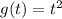
`g(t)=t^2`. Then


`\displaystyle(f*g)(t)=\int_(-\infty)^\infty u(\tau-1)(t-\tau)^2\,\mathrm d\tau`

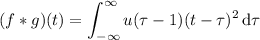
The Heaviside step function is defined as


`u(t)=\begin{cases}0&\text{for }t<0\\1&\text{for }t\ge0\end{cases}`

and adjusting its argument by 1, you have


`u(t-1)=\begin{cases}0&\text{for }t<1\\1&\text{for }t\ge1\end{cases}`

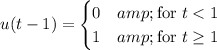
which means the integral reduces to


`(f*g)(t)=\displaystyle\int_1^\infty (t-\tau)^2\,\mathrm d\tau`

This integral doesn't converge, but hopefully it's a simple enough demonstration of how you might go about computing such an integral.