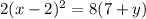Question

Which equation is the inverse of 2(x – 2)2 = 8(7 + y)?

Options:
–2(x – 2)^2 = –8(7 + y)
y= 1/4 x^2 -x -6
y= -2 +/- sqrt of 28+4x
y= 2 +/- sqrt of 28+4x


I'm leaning towards the 4th choice but...

Answer 1

The given expression is
2(x - 2)² = 8(7 + y)
Rewrite the expression as follows:
7 + y = (2/8)*(x-2)² = (1/4)*(x-2)²
y = (1/4)(x-2)² - 7

To find the inverse, switch x and y, and solve for y.
x = (1/4)(y-2)² - 7
Multiply through by 4.
4x = (y-2)² - 28
(y-2)² = 4x + 28
y - 2 = √(4x + 28)
y = 2 +/- √(4x + 28)
This expression is the inverse of the given expression.

Answer:
`y=2 \pm √(4x+28)`

Answer 2

Option 4th is correct

`y=2 \pm √(28+4x)`

Explanation:

Given the equation:

`2(x-2)^2 = 8(7+y)`

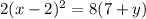
Step 1.

Interchange the variable x and y

`2(y-2)^2 = 8(7+x)`

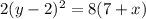
Step 2.

Solve for y in terms of x.

Divide by 2 to both sides we have;

`(y-2)^2 = 4(7+x)`

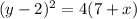
Using distributive property,
`a \cdot (b+c) =a\cdot b+ a\cdot c`

`(y-2)^2 = 28+4x`

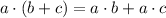
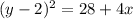
Taking square root both sides we have;

`y-2 = \pm √(28+4x)`

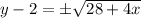
Add 2 to both sides we have;

`y=2 \pm √(28+4x)`

Therefore, equation
`y=2 \pm √(28+4x)` is the inverse of
`2(x-2)^2 = 8(7+y)`