Question

The area of a circle is directly proportional to the square

Answer 1

Proportional relationships are relationships between two variables where their ratios are equivalent. Another way to think about them is that, in a proportional relationship, one variable is always a constant value times the other.

Since the area of a circle is directly proportional to the square of the radius, their ratio should be maintained for different proportions, therefore, we have the following relation

`(50.24)/(4^2)=(A)/(6^2)`

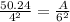
Where A represents the area of a circle with radius 6 ft. Solving for A, we have

`\begin{gathered} (50.24)/(4^2)=(A)/(6^2) \\ (50.24)/(16)=(A)/(36) \\ A=(50.24)/(16)\cdot36 \\ A=113.04 \end{gathered}`

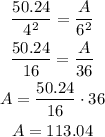
The area is 113.04 ft².