Answer:

Step-by-step explanation: We need to find the distance between the moon and earth provided the force between them and their masses. the equation used to solve this problem is as follows:
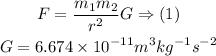
Using the known values, and plugging in the equation (1) results in:
![\begin{gathered} m_1=7.34*10^(22)\operatorname{kg} \\ m_2=5.98*10^(24)\operatorname{kg} \\ F=2.00*10^(20)N \\ \end{gathered}]()
The final step is as follows:
![\begin{gathered} (2.00*10^(20)N)=\frac{(7.34*10^(22)\operatorname{kg})\cdot(5.98*10^(24)\operatorname{kg})}{r^2}\cdot(6.674*10^(-11)m^3kg^(-1)s^(-2)_{}) \\ \text{ Rearranging} \\ r^2=\frac{(7.34*10^(22)\operatorname{kg})\cdot(5.98*10^(24)\operatorname{kg})\cdot(6.674*10^(-11)m^3kg^(-1)s^(-2)_{})}{(2.00*10^(20)N)} \\ r^2=1.4647*10^(17)m^2 \\ r=\sqrt[]{1.4647*10^(17)m^2}=3.83*10^8m \\ r=3.83*10^8m \end{gathered}]()
Therefore the distance between the moon and the earth is:
![r=3.83*10^8m]()