Question

A student bought a calculator and a textbook for a course in algebra. He told his friend that the total cost was $110 (without tax) andthat the calculator cost $50 more than three times the cost of the textbook. What was the cost of each item? Let x be the cost of thecalculator and y be the cost of the textbook.x + yThe corresponding modeling system is= 110= 3y + 50hoxUse the method of substitution to solve this system.

Answer 1

Substituting the second equation in the first one we get:

`3y+50+y=110.`

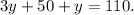
Adding like terms we get:

`4y+50=110.`

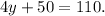
Subtracting 50 from the above equation we get:

`\begin{gathered} 4y+50-50=110-50, \\ 4y=60. \end{gathered}`

Dividing the above equation by 4 we get:

`\begin{gathered} (4y)/(4)=(60)/(4), \\ y=15. \end{gathered}`

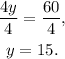
Finally, substituting y=15 in the second equation we get:

`\begin{gathered} x=3\cdot15+50, \\ x=45+50, \\ x=95. \end{gathered}`

Answer:

Cost of the calculator= $95.

Cost of the text book= $15.