Answer:
Option B -
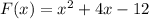
Explanation:
Given : Use the graph of
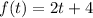 on the interval [-4, 6].
on the interval [-4, 6].
To find : Write the function F(x), where F(x)=the integral from x to 2 of f(t) dt?
Solution :
The function
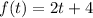
To write F(x), we integrate the function from x to 2
i.e.
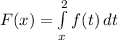
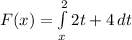
![F(x)=[2((t^2)/(2))+4t]\limits^2_x](https://img.qammunity.org/2018/formulas/mathematics/high-school/7oy0ed1p9mowesihjk2nir3uoxlagf800z.png)
![F(x)=[t^2+4t]\limits^2_x](https://img.qammunity.org/2018/formulas/mathematics/high-school/mygwvp2gay5c4qwrlxkuttnodxvl8vrtpi.png)
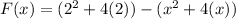
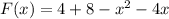
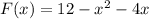
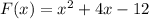
Therefore, Option B is correct.