Question

Five cards are selected without replacement from a pack of 52 playing cards. What is the probability of exactly 3 hearts?

I can find an equation for exactly 3 hearts, but I can't turn the other two cards in terms of combinatorics or permutations for some reason.

I've tried:

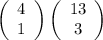
`\left(\begin{array}{cc}4\\1\end{array}\right) \left(\begin{array}{cc}13\\3\end{array}\right)` for the selection of exactly three hearts.

Thanks.

Answer 1

There are 13 total hearts in the deck, which leaves 39 non-hearts. You're drawing a hand of five cards, so the probability of getting exactly 3 hearts is


`\frac{\binom{13}3\binom{39}2}{\binom{52}5}=(2717)/(33320)`

as required.