Question

What are the solutions of (4x+1)^2-9=0

Answer 1

2 solutions: x= -1 x=
`(1)/(2)`

Explanation:

You could solve this 2 ways, either by factoring or using the quadratic formula.

Factoring:

Use the formula:
`a^2-b^2=(a-b)(a+b)`

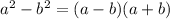
(4x+1-3)(3x+1+3)=0

(4x-2)(4x+4)=0

No we can factor out a 2 and a 4:

2(2x-1)4(x+1)=0

Divide both sides by 2x4:

(2x-1)(x+1)=0

Now set both equal to 0:

2x-1=0

x+1=0

x=
`(1)/(2)`

x=-1

For quadratic formula:

Use the formula:
`(a+b)^2=a^2+2ab+b^2`

First expand the expression:

`16x^2+8x-8=0`

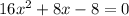
Divide both sides by 2:

`2x^2+x-1=0`

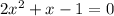
Now we can plug it in:

a=2

b=1

c=-1

`x=\frac{-1+\sqrt{1^(2) -4(2)(-1)} }{4}`

`x=(-1+√(9) )/(4)`

`x=(-1+3)/(4)`

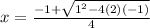
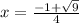
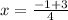
Now solve for each solution:

`x=(-1+3)/(4) \\\\x=(-1-3)/(4) \\\\x=(1)/(2)\\x=-1`

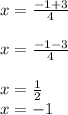
Either way you get the same answer, hope this helps! :)

Answer 2

x=1/2
x=-1
is the answer