Question

Write the equation x2 + y2 + 6x + 8y + 24 = 0 in vertex form.

Answer 1

`(x+3)^2+(y+4)^2=1`

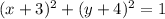
Step-by-step explanation

We want to write the equation of the circle in vertex form:

`x^2+y^2+6x+8y+24=0`

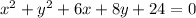
The first step is to group the x terms and y terms together and take the constant to the right-hand side of the equality sign:

`x^2+6x+y^2+8y=-24`

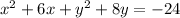
Now, complete the square for the x terms:

`\begin{gathered} x^2+6x+((6)/(2))^2+y^2+8y=-24+((6)/(2))^2 \\ x^2+6x+9+y^2+8y=-24+9 \\ (x+3)^2+y^2+8y=-15 \end{gathered}`

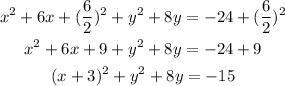
Repeat the process for the y terms:

`\begin{gathered} (x+3)^2+y^2+8y+((8)/(2))^2=-15+((8)/(2))^2 \\ (x+3)^2+y^2+8y+16=-15+16 \\ (x+3)^2+(y+4)^2=1 \end{gathered}`

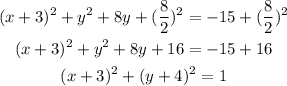
That is the equation of the circle in vertex form.