Given:
The function
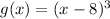
Required:
Graph g and identify what the transformation of the parent function it represents.
Step-by-step explanation:
The graph of given function and parent function:
So, the parent function is cubic and it is translated 8 units to right.
Answer:
Second option is correct.