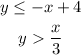Question

I need help with the problem i sent via screen shot. Please see attatchment. Thaks

Answer 1

The first step is to find the equations of the lines in slope-intercept form y=mx+b, where m is the slope and b is the y-intercept.

In the solid line, two points on the line are located at: (0,4) and (3,1).

The slope of a line is given by the following formula:

`\begin{gathered} m=(y2-y1)/(x2-x1) \\ By\text{ replacing the known values} \\ m=(1-4)/(3-0)=(-3)/(3)=-1 \end{gathered}`

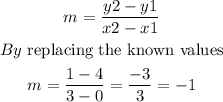
And the y-intercept is at y=4. Then b=4.

The equation of the solid line is then:

`y=-1x+4=-x+4`

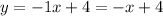
As the shaded region is below the line, then we can say that it is represented by the values that are less or equal to the line, then the first inequality is:

`y\le-x+4`

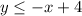
Now, let's find the equation of the dotted line.

Two points on this line are (0,0) and (3,1).

The slope of this line is:

`m=(1-0)/(3-0)=(1)/(3)`

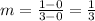
And the y-intercept is at y=0, then b=0.

The equation of the dotted line is then:

`y=(1)/(3)x+0=(x)/(3)`

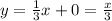
As the shaded region is over the dotted line (the dotted line means the line is not included in the solution), then the shaded region is related to the values which are greater than the line, thus the inequality is:

`y>(x)/(3)`

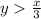
Therefore, the system of inequalities that represent the shaded portion of the graph is:

`\begin{gathered} y\le-x+4 \\ y>(x)/(3) \end{gathered}`