Question

Two small planes start from the same point and fly opposite directions. The first plane is flying 50 mph slower than the second plane. In 3 h, the planes are 780 mi apart. Find the rate of each plane.

Answer 1

Let x and y be the speeds of the first and second planes, respectively. Therefore,

`\begin{gathered} x=y-50 \\ \text{and} \\ 3(x+y)=780 \end{gathered}`

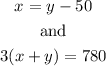
Substituting the first equation into the second one

`\begin{gathered} \Rightarrow3((y-50)+y)=780 \\ \Rightarrow3(2y-50)=780 \\ \Rightarrow6y-150=780 \\ \Rightarrow6y=930 \\ \Rightarrow y=155 \end{gathered}`

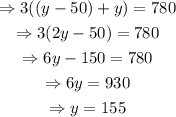
Finally, finding the value of x

`\begin{gathered} \Rightarrow x=155-50=105 \\ \end{gathered}`

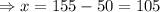
Thus, the speed of the first plane is 105mi/hr and the speed of the second plane is 155mi/hr