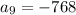Question

Instructions: For the following sequence, state the common ratio, identify which is the explicit form and which is the recursive form of the rule, and find the term listed.

Answer 1

Given the sequence;

`-3,6,-12,24`

The common ratio is the ratio between two consecutive numbers in a geometric sequence.

Thus;

`\begin{gathered} r=(a_2)/(a_1)=(a_3)/(a_2) \\ \\ r=(6)/(-3) \\ \\ r=-2 \end{gathered}`

Common Ratio:

`r=-2`

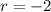
Also, given the formula;

`a_n=-3\cdot(-2)^(n-1)`

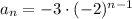
The formula is an explicit formula of the geometric sequence.

The recursive formula is;

`\begin{gathered} a_n=r(a_(n-1)) \\ \\ a_n=-2(a_(n-1)) \end{gathered}`

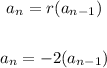
Then, the ninth term is;

`\begin{gathered} n=9 \\ \\ a_9=-3\cdot(-2)^(9-1) \\ \\ a_9=-3\cdot(-2)^8 \\ \\ a_9=-3(256) \\ \\ a_9=-768 \end{gathered}`

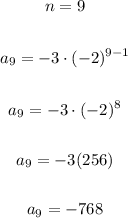
The ninth term is;

`a_9=-768`