Question

Quadrilateral R was transformed to create its image, quadrilateral R', as shownon this coordinate plane.

Answer 1

Step 1:Write out the coordinates of the vertices of the objects and its images

Let the vertices of R be ABCD such that

A ( -9 , 3) B ( -5 , 7) C (-3 , 5) D (-5 , 2)

Let the vertices of R' be A'B'C'D' such that

A' (9 ,-6) B' (5 , -2) C' (3 , -4) D' (5 , -7)

Step 2: Reflect the object R about the y-axis

The reflection rule about the y-axis is given by

`(x,y)\to(-x,y)`

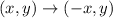
Let the corresponding image of R after reflection about the y-axis be the quadrialteral A'B'C'D'. Hence,

`\begin{gathered} \text{ the coordinates of A' }=(-(-9),3)=(9,3) \\ \text{ the coordinates of B' }=(-(-5),7)=(5,7) \\ \text{ the coordinates of C' }=(-(-3),5)=(3,5) \\ \text{ the coordinates of D' }=(-(-5),2)=(5,2) \end{gathered}`

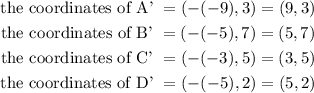
Step 3: Translate the quadrilateral A'B'C'D' down by 9 units.

The rule for translation down by 9 units is given by

`(x,y)\to(x,y-9)`

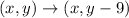
Let the corresponding image of A'B'C'D' after translation down the y-axis be the quadrialteral A''B''C''D''.

`\begin{gathered} \text{ the coordinates of A'' }=(9,3-9)=(9,-6) \\ \text{ the coordinates of B'' }=(5,7-9)=(5,-2) \\ \text{ the coordinates of C'' }=(3,5-9)=(3,-4) \\ \text{ the coordinates of D'' }=(5,2-9)=(5,-7) \end{gathered}`

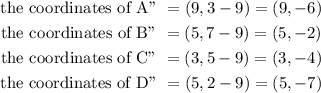
Hence, the coordinates of the vertices of the quadrialteral A''B''C''D'' corresponds to the coordinates of the vertices of R' .

Therefore, a translation 9 units down followed by a reflection over the y -axis, Option A is the correct answer