Question

The driver of a red car decides to pass another car on a two-lane road. While passing, a black car appears in the passing lane approaching the red car from the other direction. As indicated by the speedometers, the speed of the red car is 69 mph and the speed of the black car is 58 mph. From the perspective of the red car, what is the speed of the black car?

Answer 1

68 mph will be the speed

Answer 2

v = 127 mph

Step-by-step explanation:

As we know that when we observe the motion of a moving object from a reference frame which itself is moving then it is known as relative motion.

So here we know that

velocity of red car is given as

`\vec v_1 = 69 mph \hat i`

now it is given that black car is moving opposite to red car with the speed

`\vec v_2 = 58 mph (-\hat i)`

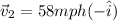
now we have to find the relative velocity of black car with respect to Red car

now we will have

`\vec v_(21) = \vec v_2 - \vec v_1`

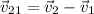
now we will have

`\vec v_(21) = 58 mph(-\hat i) - 69 mph(\hat i)`

`\vec v_(21) = 127 mph (-\hat i)`

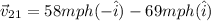
so it appears to come at speed of 127 mph from opposite side