Question

A bond is initially bought for 250. It doubles in value every decade.

Answer 1

We have a bond that doubles it value every decade.

Initially, at decade=0, its value is 250.

Then, if it doubles, we will have:

`\begin{gathered} V(1)=2\cdot V(0)=2\cdot250=500 \\ V(2)=2\cdot V(1)=2\cdot500=1000 \\ V(3)=2\cdot V(2)=2\cdot1000=2000 \end{gathered}`

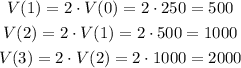
We can generalize this formula as:

`\begin{gathered} V(1)=2\cdot V(0) \\ V(2)=2\cdot V(1)=2\cdot(2\cdot V(0))=2^2\cdot V(0) \\ V(3)=2\cdot V(2)=2\cdot(2^2\cdot V(0))=2^3\cdot V(0) \\ V(d)=2^d\cdot V(0)=2^d\cdot250=250\cdot2^d \end{gathered}`

We can find the amount of decades that it takes for the bond to reach a value of $10,000 using the equation for V(d):

`\begin{gathered} V(d)=10000 \\ 250\cdot2^d=10000 \\ 2^d=(10000)/(250) \\ 2^d=40 \\ d=\log _2(40)\approx5.32\approx6 \end{gathered}`

It will take 6 decades for the bond to have a value that is more than $10,000.

Answer:

1)

Decades since bond is bought | Dollar value of bond

0 | 250

1 | 500

2 | 1000

3 | 2000

d | 250*2^d

2) It will take 6 decades for the bond to have a value that is more than $10,000.

3) V(d)=250*2^d