Question

I have a practice question that I need to explain and answered.The product of the matrices IS or IS NOT the identity matrix Therefore, X and A ARE or ARE NOT inverses of each other.

Answer 1

To know if two matrices product is or is not the identity, we need to multiply it. And given matrices A and X, let's do it.

The multiplication of two matrices 2x2 is given by:

`\begin{bmatrix}{A_(11)} & A_(12) & {} \\ A_(21) & A_(22) & {} \\ & {} & {}\end{bmatrix}*\begin{bmatrix}{B_(11)} & B_(12) & {} \\ B_(21) & B_(22) & {} \\ & {} & {}\end{bmatrix}=\begin{bmatrix}{C_(11)} & C_(12) & {} \\ C_(21) & C_(22) & {} \\ & {} & {}\end{bmatrix}`

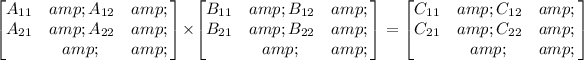
where:

`C_(ij)=\sum ^2_(n\mathop=1)A_(in)* B_(nj)`

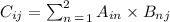
Now, we calculate the terms of X A:

`C_(11)=X_(11)* A_(11)+X_(12)* A_(21)=2*(1)/(2)+(-1)*(-2)=1+2=3`

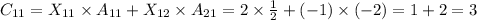
Because we know that a 2x2 identity matrix is given by:

`I=\begin{bmatrix}{1} & 0 & {} \\ {0} & 1 & {} \\ {} & {} & {}\end{bmatrix}`

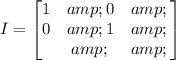
and the term C₁₁ is different from 1, we can already conclude that the product of the two matrices IS NOT the identity matrix.

We say two matrices are inverse of each other when the multiplication of them results in the identity matrix, doesn't matter the order. And because we already saw above that XxA will not result in the identity matrix, X and a are not inverse of each other.