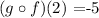Question:
Solution:
Consider the following functions:
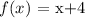
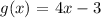
then:
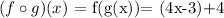
this is equivalent to:
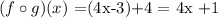
thus:

So, replacing x = 2 in the previous function we get:
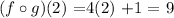
then:
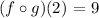
On the other hand, the composition:
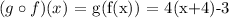
this is equivalent to:
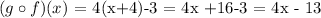
then, we can conclude that:
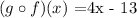
So, replacing x = 2 in the previous function we get:
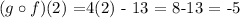
then:
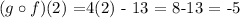
then:
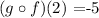
Then the correct answers are:
1)

2)
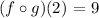
3)
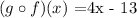
4)