Question

Dr. John Paul Stapp was U.S. Air Force officer who studied the effects of extreme deceleration on the human body. On December 10, 1954, Stapp rode a rocket sled, accelerating from rest to a top speed of 282 m/s (1015 km/h) in 5.00 s, and was brought jarringly back to rest in only 1.40 s! Calculate his (a) acceleration and (b) deceleration. Express each in multiples of g (9.80 m/s2) by taking its ratio to the acceleration of gravity.Answers from book. A. 56.4 M/S2 OR 5.76G B. 201 M/S2 OR 20.6G

Answer 1

Answers:

(a) 56.4 m/s² or 5.76g.

(b) 201.4 m/s² or 20.6g.

Step-by-step explanation:

The acceleration of an object can be calculated as:

`a=(v_f-v_i)/(t)`

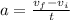
Where vf is the final velocity, vi is the initial velocity and t is the time that takes to go from vi to vf.

Then, the rocket sled accelerates from rest to 282 m/s in 5.00 s. It means that the initial velocity was 0 m/s, the final velocity was 282 m/s and the time was 5.00s, so the acceleration was equal to:

`a=\frac{282\text{ m/s - 0 m/s}}{5\text{ s}}=(282)/(5)=56.4m/s^2`

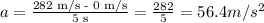
Now, to write the acceleration in terms of gravity, we need to divide 56.4 m/s² by 9.80 m/s², so:

`(56.4)/(9.8)=5.76`

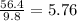
Therefore, 56.4 m/s² is equivalent to 5.76g.

On the other hand, if he changes the velocity from 282 m/s to 0m/s in 1.40s, the acceleration was:

`a=\frac{0\text{ m/s - 282 m/s}}{1.40\text{ s}}=(-282)/(1.40)=-201.4m/s^2`

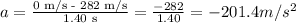
It means that the deceleration was equal to 201.4 m/s². Then, if we divide 201.4 by 9.8, we get:

`(201.4)/(9.8)=20.6`

Therefore, 201.4 m/s² is equivalent to 20.6g.