Given,
The coefficient of thermal expansion of iron, α₁=11.8×10⁻⁶ °C⁻¹
The coefficient of thermal expansion of copper, α₂=16.5×10⁻⁶ °C⁻¹
The length of both strips, L=10 cm=0.1 m
The initial temperature, T₁=20 °C
The final temperature, T₂=100 °C
The increase in the length due to change in the temperature is given by,
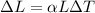
Thus, the change in the length of the iron strip is,
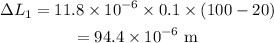
Therefore the new length of the iron strip when the temperature rises to 100 °C is
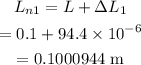
The change in the length of the copper strip is given by,

Thus the new length of the copper strip is,
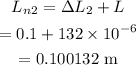
Thus the difference in the new lengths of the two metal strips is
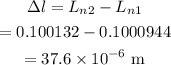
Thus the change in the length of the two metal strips when the temperature is increased to 100 °C is 37.6×10⁻⁶ m.