ANSWERS
a. N(60, 121)
b. N(60, 121/12)
c. P(59.3 < X < 61.2) = 0.0677
d. P(59.3 < X < 61.2) = 0.2351
e. Yes
Step-by-step explanation
Given:
• Mean; 60 mL
,
• Standard deviation: 11 mL
,
• 12 randomly selected people are observed pouring syrup on their pancakes.
a. The distribution of X is,
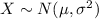
So this is,
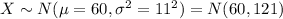
Hence, the distribution of X is N(60, 121).
b. The distribution of the x (suppose the line is above x instead) is,
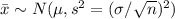
So, if 12 people are randomly chosen,
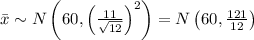
Hence, the distribution of x is N(60, 121/12).
c. We have to find the probability that a randomly chosen individual consumes between 59.3 mL and 61.2 mL of syrup. This is,
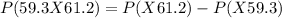
Using the standardization formula,
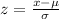
We have,
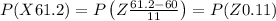
And,
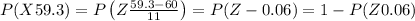
We look up these z-scores in a z-table,
So,
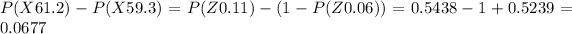
Hence, the probability that a randomly selected person consumes between 59.3 mL and 61.2 mL of syrup is 0.0677.
d. Now, for the entire group of 12 pancake eaters, we have to find the probability that the average amount of syrup is between 59.3 mL and 61.2 mL (same as part c, but for x). This is,
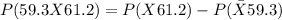
Standardize with,
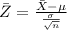
So we have,
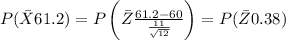
And,
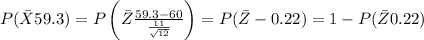
Again, we look up these values in a z-table,
So,
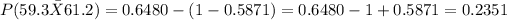
Hence, the probability that the average amount of syrup is between 59.3 mL and 61.2 mL is 0.2351.
e. Yes, it is necessary for part (d) the assumption that the distribution is normal.