Question

A 0.2 ml dose of a drug is injected into a patient steadily for 0.4 seconds. At the end of this time, the quantity, , of the drug in the body starts to decay exponentially at a continuous rate of 0.4 percent per second. Using formulas, express as a continuous function of time, , in seconds.

Answer 1

We have to model the exponential decay of the drug quantity Q.

The time t = 0 will correspond to the moment where the dose has been injected totally.

The value of Q at time t = 0, that is Q(0), then has a value:

`Q(0)=0.2`

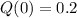
Then, the value of Q decays exponentially. The rate is 0.4% per second.

We can start expressing the general model for Q:

`Q(t)=A\cdot b^t`

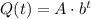
where A and b are parameters of the model.

We can find A as:

`\begin{gathered} Q(0)=Ab^0 \\ Q(0)=A\cdot1 \\ Q(0)=A \\ A=0.2 \end{gathered}`

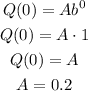
Parameter A correspond to the initial value of Q(0), which is 0.2 ml.

Now, we will use the rat of change of Q to find the parameter k.

As Q decays by 0.4% per second, we can write:

`\begin{gathered} Q(t+1)=(1-(0.4)/(100))\cdot Q(t) \\ Q(t+1)=(1-0.004)\cdot Q(t) \\ Q(t+1)=0.996\cdot Q(t) \end{gathered}`

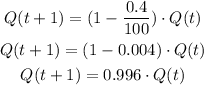
Then, we can rearrange it as:

`\begin{gathered} (Q(t+1))/(Q(t))=0.996 \\ \frac{0.2\cdot b^(t+1)}{0.2\cdot b^t^{}}=0.996 \\ b^(t+1-t)=0.996 \\ b^1=0.996 \\ b=0.996 \end{gathered}`

We then can express the model for Q as:

`Q(t)=0.2\cdot0.996^t`

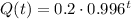
Answer: Q(t) = 0.2*(0.996)^t