Question

Which of the following are the coordinates of the image of (5,-10) after a 180 degree rotation about (-3,1)?(1) (-11,12)(2) (-5,10)(3) (13,-21)(4) (2,-9)

Answer 1

When rotating an image about a point not in the origin, we first subtract the coordinates of the point of the image to the cooridinates of the point of rotation.

We get,

Original point: (5, -10)

Point of rotation: (-3, 1)

New coordinate: [5 - (-3), -10 - (1)] = (8, -11)

At 180 Degree rotation,

`\text{ A(x,y) }\rightarrow\text{ A'(-x,-y)}`

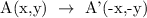
We get,

`\text{ (x,y) = (8,-11) }\rightarrow\text{ (x',y') = \lbrack-(8), -(-11)\rbrack}`
`Initial\text{ Transformation, (x',y') = (-8,11)}`

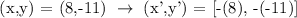
For the final transformation, let's add back the point of rotation to the transformed points:

`\text{ (x'y') = \lbrack-8 + (-3), 11 + 1\rbrack = (-8 - 3 , 11 + 1)}`
`\text{ Therefore, (x'y') = -11, 12}`

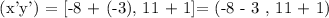
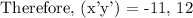
Therefore, the answer is 1 : (-11,12).