Question

if we remove all of the queens and Jack's from a 52 card deck, how many unique four card combinations can we create?

Answer 1

Answer:

135751 unique four card combinations can be created

Explanations:

Total number of cards in a deck = 52

Number of queens in a deck = 4

Number of jacks in a deck = 4

If all the queens and jacks are removed, number of remaining cards = 52 - 8

Number of remaining cards = 44

Number of unique four card combinations that can be created = 44C4

`nC_r=\text{ }(n!)/((n-r)!r!)`

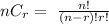
Therefore:

`\begin{gathered} 44C_4=\text{ }(44!)/((44-4)!4!) \\ 44C_4=\text{ }(44!)/(40!4!) \\ 44C_4=\text{ }(44*43*42*41*40!)/(40!*4*3*2*1) \\ 44C_4=\text{ }(3258024)/(24) \\ 44C_4=\text{ }135751 \end{gathered}`

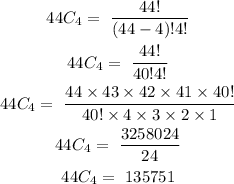
135751 unique four card combinations can be created