Question

Find the value of the following expression: (28.5-5. 190)-2 2 228 (5 points) Write your answer in simplified form. Show all of your steps. (5 points)

Answer 1

We are asked to reduce a product of the power expressions shown below:

`(2^8\cdot5^(-5)\cdot19^0)^(-2)\cdot((5^(-2))/(2^3))^4\cdot2^(28)`

So we start by recalling that any number different from zero to the power "0" (zero gives "1" (one), so we replace 19 to the power zero with a "1".

So, now, inside the first parenthesis we have 2 to the power 8 and 5 to the power "-5". Both these powers will be multiplied by the power "-2" outside the parenthesis . Then we end up for this first expression with: 2 to the power "-16" and 5 to the power "+10". 2^(-16) 5^(10)

Now the next parenthesis that involves a fraction:

the numerator (5^-2) becomes 5 to the power "-8" when applying the power of a power property of exponents. And the denominator becomes: 2 to the power 12. Now, we can move this denominator to the numerator by changing the sign of the power. Thus now we have 2 to the power "-12" in the numerator.

This middle expression is: 5^(-8) 2^(-12)

Since the last expression is already reduced 2^(28), we now have the following product:

`2^(-16)\cdot5^(10)\cdot5^(-8)\cdot2^(-12)\cdot2^(28)=2^(-28+28)\cdot5^(10-8)=5^2=25`

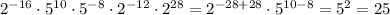
So we see that all powers of the base 2 simplify to reduce it to 2 to the power zero = 1. While the only base that remains is base 5 to the power "2".

The final reduced answer is then 5 to the power 2 which is 25.