Answer:
7
Step-by-step explanation:
From the question, we're told that triangles AMY and MEG are similar. If triangle AMY has sides AM = 5, MY = 7, and AY = 3 then we can find the side lengths of triangle MEG since we're told from the question that it is a dilation of AMY by a scale factor of 1/3.
So all we need to is multiply the corresponding sides of AMY by 1/3, so we'll have;

We can then go ahead and find the perimeter of MEG. Note that to find the perimeter of a triangle, we add all the length of its sides;
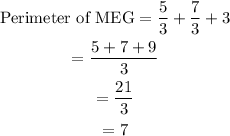
The perimeter of MEG is 7.