Question

The price of 9-volt batteries is increasing according to thefunction below, where t is years after January 1, 1980. Duringwhat year will the price reach $4?

Answer 1

In the equation given, P(t) represents the price of the batteries. We want to figure out what t is equal to when P(t) is 4. In order to do that, we can set up the following equation:

`4=1.1*e^(0.047t)`

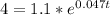
We need to figure out how to isolate t. we could start by dividing both sides by 1.1 to isolate the term that contains e

`\begin{gathered} (4)/(1.1)=e^(0.047t) \\ 3.636363=e^(0.047t) \end{gathered}`

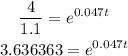
Now, we need to isolate t. We can do this by taking the natural log of both sides (the natural log is just a special logarithmic function in which the base is e):

`\ln(3.636363)=\ln(e^(0.047t))`

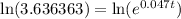
Using our log rules, we can bring 0.047t to the front because it is a power:

`\ln(3.636363)=0.047t*\ln(e)`

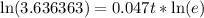
because ln is the same thing as log base e, we know that ln(e) has to be equal to 1 (you can think about it this way: e^1 is e, which means ln(e) is 1). Therefore, we can simplify it to get the following equation:

`\ln(3.636363)=0.047t`

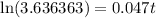
Now, we can use a calculator to solve for t:

`\begin{gathered} t=(\ln(3.636363))/(0.047) \\ t\approx27\text{ years} \end{gathered}`

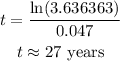
We are looking for the year when the price is 4 dollars, and we have figured out that the year will be 27 years after 1980. In other words, it will be 1980 + 27, or 2007

Therefore, the price will reach $4 in 2007