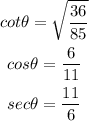Question

Find cot, cos0, and sect, where o is the angle shown in the figure.Give exact values, not decimal approximations.

Answer 1

Given:

A triangle is given as below

Find:

we have to find the values of cotangent, cosine and secant at theta.

Step-by-step explanation:

we know,

`\begin{gathered} cos\theta=(Base)/(Hypotenuse)=(6)/(11) \\ sec\theta=(1)/(cos\theta)=(1)/((6)/(11))=(11)/(6) \\ tan^2\theta=sec^2\theta-1=(121)/(36)-1=(85)/(36) \\ cot^2\theta=(1)/(tan^(^2)\theta)=(1)/((85)/(36))=(36)/(85) \\ cot\theta=\pm\sqrt{(36)/(85)} \end{gathered}`

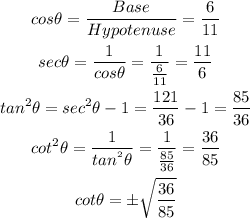
since, angle is less than 90 degree, so we will take only positive value of cotangent,

Therefore, the required values are given as below

`\begin{gathered} cot\theta=\sqrt{(36)/(85)} \\ cos\theta=(6)/(11) \\ sec\theta=(11)/(6) \end{gathered}`