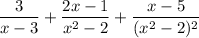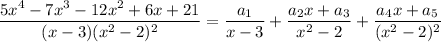
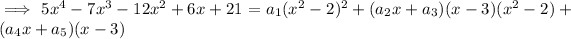
When
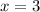
, you're left with
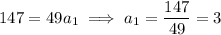
When
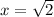
or
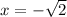
, you're left with
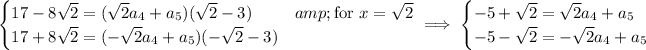
Adding the two equations together gives
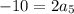
, or
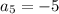
. Subtracting them gives
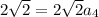
,
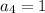
.
Now, you have
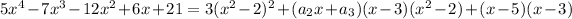
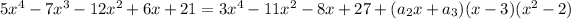
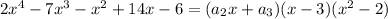
By just examining the leading and lagging (first and last) terms that would be obtained by expanding the right side, and matching these with the terms on the left side, you would see that
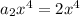
and
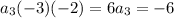
. These alone tell you that you must have
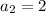
and
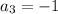
.
So the partial fraction decomposition is