Question

Use the Factor Theorem to determine whether x+2 is a factor of P(x) = -x - 3x² - 7.Specifically, evaluate P at the proper value, and then determine whether x + 2 is a factor.P(O) = 0O x + 2 is a factor of P(x)0 x + 2 is not a factor of P(x)

Answer 1

According to the factor theorem, for any polynomial P(x), (x - a) is a factor if P(a) = 0.

The term (x - a) in this case is (x + 2), meaning that -a = 2, or a = -2.

Now, when evaluating P(-2), that is, replacing -2 anywhere we see an x, we should obtain 0 if (x + 2) is a factor of the polynomial given. Otherwise, it is not a factor.

`\begin{gathered} P(x)=-x^3-3x^2-7 \\ P\mleft(-2\mright)=-\mleft(-2\mright)^3-3\mleft(-2\mright)^2-7 \\ P(-2)=-(-8)-3(4)-7 \\ P(-2)=8-12-7 \\ P(-2)=-11 \end{gathered}`

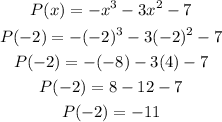
Then:

P(-2) = -11.

Having that P(a) is not 0, we can say that (x + 2) is not a factor of P(x)