Given data:
* The mass of the boulder is m = 200 kg.
* The height in the given case is h = 1000 m.
Solution:
(a). The potential energy of boulder, when it is 1000 m from the ground is,
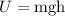
where g is the acceleration due to gravity,
Substituting the known values,
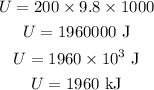
Thus, the potential energy of the boulder in the given case is 1960 kJ.
(b). The kinetic energy of the boulder at the maximum height (1000 m) in the rest state is zero.
Thus, the kinetic energy of the boulder when it is 1000-m above the ground is 0 J.
(c). The potential energy of the boulder above 500 m is,
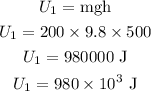
By simplifying,
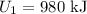
Thus, the potential energy of the boulder in the given case is 980 kJ.
As the boulder starts moving, some part of the potential energy is converted into kinetic energy.
Thus, the lost potential energy gets converted into kinetic energy.
(d). The net energy of the boulder at 1000 m is,
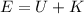
where U is the potential energy at height 1000 m and K is the kinetic energy of the boulder at height 1000 m,
Substituting the known values,
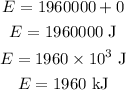
According to the law of conservation of energy, the net energy of the system remains conserved at a height of 500 m.
Thus, the kinetic energy of the boulder at height 500 m is,
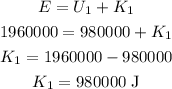
By simplifying,

Thus, the kinetic energy of the boulder at a height of 500 m is 980 kJ.
(e). The potential energy of the boulder just before hitting the ground is zero as the height of the boulder is zero.
Thus, the kinetic energy of the boulder just before hitting the ground is,
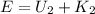
where U_2 is the potential energy before hitting the ground, K_2 is the kinetic energy just before hitting the ground, and E is the net energy,
Substituting the known values,
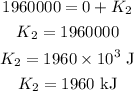
Thus, the kinetic energy just before hitting the ground is 1960 kJ.