Question

The curve with equation y=e^2x/4+3e^x has one stationary point.find the exact value of the coordinates of this point

Answer 1

`y=(e^(2x))/(4+3e^x)`

`\implies y'=(2e^(2x)(4+3e^x)-3e^xe^(2x))/((4+3e^x)^2)`

`\implies y'=(8e^(2x)+3e^(3x))/((4+3e^x)^2)`

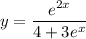
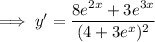
Stationary points occur where the derivative is zero. The denominator is positive for all
`x`, so we only need to worry about the numerator.


`8e^(2x)+3e^(3x)=e^(2x)(8+3e^x)=0`


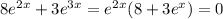
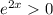
`e^(2x)>0` for all
`x`, so we can divide through:


`8+3e^x=0\implies e^x=-\frac83`

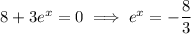
But
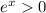
`e^x>0` for all
`x\in\mathbb R`, so this function has no stationary points...

I suspect there may be a typo in the question.