Question

Estimate the rate of change of f(x) = 35(0.7)^x at x = 0.

Answer 1

To find the rate of change we need to find the derivative of the function. The derivative of an exponential function is:

`(d)/(dx)a^x=a^x\ln a`

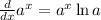
Then in our case we have:

`\begin{gathered} (d)/(dx)\lbrack35(\text{0}.7)^x\rbrack=35(d)/(dx)(0.7)^x \\ =35(0.7)^x\ln 0.7 \\ =35\ln 0.7(0.7)^x \end{gathered}`

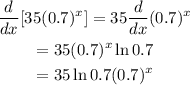
Now we evaluate the derivative at the point x=0, then:

`35\ln \text{0}.7(\text{0}.7)^0=-12.4836`

Therefore the rate of change is appoximately -12.4836.