Question

Which is true about the degree of the sum and difference of the polynomials 3x5y – 2x3y4 – 7xy3 and –8x5y + 2x3y4 + xy3?

Answer 1

The sum of the degree of 6 but the difference has a degree of 7.

Answer 2

6 is the degree of the sum of the polynomials

7 is the degree of the difference of the polynomials

Explanation:

3x^5y – 2x^3y^4 – 7xy^3 and –8x^5y + 2x^3y^4 + xy^3

First we find the sum of the polynomials

`3x^5y – 2x^3y^4 – 7xy^3 + –8x^5y + 2x^3y^4 + xy^3`

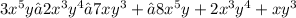
Combine like terms

3x^5y - 8x^5y = -5x^5y (degree = 6)

– 2x^3y^4 + 2x^3y^4 =0

– 7xy^3+ xy^3= -6xy^3 (degree= 4)

So sum of the polynomials becomes

-5x^5y -6xy^3

For degree we add the exponents

highest degree = 6

So 6 is the degree of the sum of the polynomials

Now we find the difference

`3x^5y – 2x^3y^4 – 7xy^3 - (–8x^5y + 2x^3y^4 + xy^3)`

`3x^5y – 2x^3y^4 – 7xy^3 + 8x^5y -  2x^3y^4 - xy^3)`

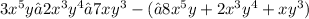
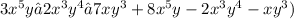
Combine like terms

3x^5y + 8x^5y = 11x^5y (degree = 6)

– 2x^3y^4 - 2x^3y^4 =-4x^3y^4 (degree = 7)

– 7xy^3- xy^3= -8xy^3 (degree= 4)

So difference of the polynomials becomes

11x^5y-4x^3y^4 -8xy^3

For degree we add the exponents

highest degree = 7

So 7 is the degree of the difference of the polynomials